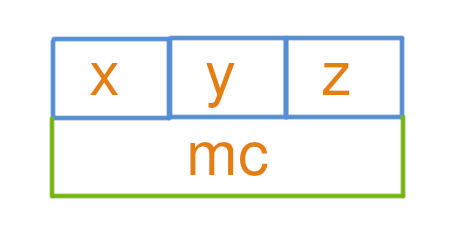该篇内容基于小彭老师访存优化课程,添加了自己的理解和备注
第0章:前言
将会用到的工具代码:
ticktock.h封装TBB计时工具
1
2
3
4
5
6
7
8
9
10
11
12
13
| #pragma once
#include <tbb/tick_count.h>
#define TICK(x) auto bench_##x = tbb::tick_count::now();
#define TOCK(x) \
std::cout << #x ": " << (tbb::tick_count::now() - bench_##x).seconds() \
<< "s" << std::endl;
|
- Google性能测试工具benchmark模板
- 关于benchmark工具的使用请自行学习
- (把要测试的部分放到指定的
for (auto _ : bm)循环就可以了)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
| #include <benchmark/benchmark.h>
#include <omp.h>
#include <x86intrin.h>
#include <array>
#include <cmath>
#include <cstdlib>
#include <cstring>
#include <iostream>
#include <vector>
void BM_fill(benchmark::State &bm) {
for (auto _ : bm) {
}
}
BENCHMARK(BM_fill);
BENCHMARK_MAIN();
|
- pod 模板类,使得 vector 的 resize 不会零初始化其中的值
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
| #pragma once
#include <new>
#include <utility>
template <class T>
struct pod {
private:
T m_t;
public:
pod() {}
pod(pod &&p) : m_t(std::move(p.m_t)) {}
pod(pod const &p) : m_t(p.m_t) {}
pod &operator=(pod &&p) {
m_t = std::move(p.m_t);
return *this;
}
pod &operator=(pod const &p) {
m_t = p.m_t;
return *this;
}
pod(T &&t) : m_t(std::move(t)) {}
pod(T const &t) : m_t(t) {}
pod &operator=(T &&t) {
m_t = std::move(t);
return *this;
}
pod &operator=(T const &t) {
m_t = t;
return *this;
}
operator T const &() const { return m_t; }
operator T &() { return m_t; }
T const &get() const { return m_t; }
T &get() { return m_t; }
template <class... Ts>
pod &emplace(Ts &&...ts) {
::new (&m_t) T(std::forward<Ts>(ts)...);
return *this;
}
void destroy() { m_t.~T(); }
};
|
案例:
运行下面的代码:
- 针对你的运行环境不同,可能需要测试其他值才能观察到现象
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
| #include <iostream>
#include <vector>
#include "ticktock.h"
constexpr size_t n = 1 << 22;
int main() {
std::vector<int> arr(n);
TICK(write_0);
for (size_t i = 0; i < n; i++) {
arr[i] = 0;
}
TOCK(write_0);
TICK(write_1);
for (size_t i = 0; i < n; i++) {
arr[i] = 1;
}
TOCK(write_1);
return 0;
}
|
我们会发现,在当前运行环境下,当数组大小小于CPU缓存时,写入0与写入1的速度有着一倍差距;但是数组大小大于(或者接近)缓存时,两者写入时间又区别不大。
本篇我们就来探讨这个现象
第1章:内存带宽
cpu-bound 与 memory-bound
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
| #include <benchmark/benchmark.h>
#include <omp.h>
#include <x86intrin.h>
#include <array>
#include <cmath>
#include <cstdlib>
#include <cstring>
#include <iostream>
#include <vector>
constexpr size_t n = 1 << 26;
std::vector<float> a(n);
void BM_fill(benchmark::State &bm) {
for (auto _ : bm) {
for (size_t i = 0; i < n; i++) {
a[i] = 1;
}
}
}
BENCHMARK(BM_fill);
void BM_parallel_fill(benchmark::State &bm) {
for (auto _ : bm) {
#pragma omp parallel for
for (size_t i = 0; i < n; i++) {
a[i] = 1;
}
}
}
BENCHMARK(BM_parallel_fill);
void BM_sine(benchmark::State &bm) {
for (auto _ : bm) {
for (size_t i = 0; i < n; i++) {
a[i] = std::sin(i);
}
}
}
BENCHMARK(BM_sine);
void BM_parallel_sine(benchmark::State &bm) {
for (auto _ : bm) {
#pragma omp parallel for
for (size_t i = 0; i < n; i++) {
a[i] = std::sin(i);
}
}
}
BENCHMARK(BM_parallel_sine);
BENCHMARK_MAIN();
|
通常来说,并行只能加速计算的部分,不能加速内存读写的部分。
因此,对 fill 这种没有任何计算量,纯粹只有访存的循环体,并行没有加速效果。称为内存瓶颈(memory-bound)。
而 sine 这种内部需要泰勒展开来计算,每次迭代计算量很大的循环体,并行才有较好的加速效果。称为计算瓶颈(cpu-bound)。
并行能减轻计算瓶颈,但不减轻内存瓶颈,故后者是优化的重点。
浮点加法的计算量
- 冷知识:并行地给浮点数组每个元素做一次加法反而更慢。
- 修改上面
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
| #include <benchmark/benchmark.h>
#include <omp.h>
#include <x86intrin.h>
#include <array>
#include <cmath>
#include <cstdlib>
#include <cstring>
#include <iostream>
#include <vector>
constexpr size_t n = 1 << 28;
std::vector<float> a(n);
void BM_serial_add(benchmark::State &bm) {
for (auto _ : bm) {
for (size_t i = 0; i < n; i++) {
a[i] = a[i] + 1;
}
benchmark::DoNotOptimize(a);
}
}
BENCHMARK(BM_serial_add);
void BM_parallel_add(benchmark::State &bm) {
for (auto _ : bm) {
#pragma omp parallel for
for (size_t i = 0; i < n; i++) {
a[i] = a[i] + 1;
}
benchmark::DoNotOptimize(a);
}
}
BENCHMARK(BM_parallel_add);
BENCHMARK_MAIN();
|
可以看到并行后速度反而变慢了
因为一次浮点加法的计算量和访存的超高延迟相比实在太少了。
计算太简单,数据量又大,并行只带来了多线程调度的额外开销。
经验公式:1次浮点读写 ≈ 8次浮点加法
如果矢量化成功(SSE):1次浮点读写 ≈ 32次浮点加法
如果CPU有4核且矢量化成功:1次浮点读写 ≈ 128次浮点加法
常见操作所花费的时间
| 操作 |
CPU周期(大约) |
| Add, Sub, And, Or |
< 1 |
| Memory write |
≈ 1 |
| “right” branch of “if” |
≈ 1 |
| Mul |
3 - 6 |
| L1 read |
4 |
| L2 read |
10 - 12 |
| “wrong” branch of “if” |
10 - 20 |
| L3 read |
30 - 50 |
| Div |
20 - 100 |
| Function call |
25 - 250 |
| Addition polymorphic function call |
20 - 30 |
| Mutex lock/unlock |
50+ |
| Main RAM read |
100 - 150 |
| NUMA: different socket L3 read |
100 - 200 |
| NUMA: different socket RAM read |
200 - 300 |
| Allocation deallocation pair |
200+ |
| User to kernel switch and back |
300 - 500 |
| Exception throw + caught |
1000 - 2000 |
| Context switch (direct cost) |
2000 |
| Context switch (total costs, including cache invalidation) |
10K - 1M |
| Disk read |
400K+ |
表中加法(add)和乘法(mul)均指整数运算。浮点数的加法和乘法速度基本相同。
L1/L2/L3缓存读取和主内存读取的时间指读取一个缓存行(64字节)所需的CPU周期数。
根据计算:125/64*4 ≈ 8,即从主内存读取一次float大约耗费8个周期,与我们上边提到的经验公式一致。
“right”和“wrong”分别表示分支预测成功和失败的情况。
多少计算量才算多?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
| #include <benchmark/benchmark.h>
#include <omp.h>
#include <x86intrin.h>
#include <array>
#include <cmath>
#include <cstdlib>
#include <cstring>
#include <iostream>
#include <vector>
constexpr size_t n = 1 << 28;
std::vector<float> a(n);
static float func(float x) {
return x * (x * x + x * 3.14f - 1 / (x + 1)) + 42 / (2.718f - x);
}
void BM_serial_func(benchmark::State &bm) {
for (auto _ : bm) {
for (size_t i = 0; i < n; i++) {
a[i] = func(a[i]);
}
benchmark::DoNotOptimize(a);
}
}
BENCHMARK(BM_serial_func);
void BM_parallel_func(benchmark::State &bm) {
for (auto _ : bm) {
#pragma omp parallel for
for (size_t i = 0; i < n; i++) {
a[i] = func(a[i]);
}
benchmark::DoNotOptimize(a);
}
}
BENCHMARK(BM_parallel_func);
BENCHMARK_MAIN();
|
我们看上边的 func,够复杂了吧?也只是勉勉强强追上一点内存的延迟了,但在8个物理核心上并行加速后,还是变成mem-bound了。
加速比:1.01 倍(甚至在误差范围)
应该达到 8 倍(物理核心数量)才算理想加速比。
加速曲线
针对下面三个函数分别测试:
- 提示:现代CPU性能都较高,你的测试结果可能和我不一样
- 将系统设置为能效模式,限制CPU频率更容易复现结果
1
2
3
4
5
6
7
8
9
10
11
| static float funcA(float x) { return sqrtf(x) * x; }
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
| static float funcB(float x) {
return x * (x * sqrtf(x) * (x + 1) + x * 3.14f - 1 / (x + sqrtf(x - 2) + 1)) +
42 / (2.718f - x * sqrtf(x));
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
| static float funcC(float x) {
return sinf(x) + cosf((x + 1) * x) * sqrtf(x * (x + 1));
}
|
主框架:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
| #include <benchmark/benchmark.h>
#include <omp.h>
#include <x86intrin.h>
#include <array>
#include <cmath>
#include <cstdlib>
#include <cstring>
#include <iostream>
#include <vector>
constexpr size_t n = 1 << 28;
std::vector<float> a(n);
static float funcC(float x) {
return sinf(x) + cosf((x + 1) * x) * sqrtf(x * (x + 1));
}
void BM_1funcC(benchmark::State &bm) {
for (auto _ : bm) {
omp_set_num_threads(1);
#pragma omp parallel for
for (size_t i = 0; i < n; i++) {
a[i] = funcC(a[i]);
}
benchmark::DoNotOptimize(a);
}
}
BENCHMARK(BM_1funcC);
void BM_2funcC(benchmark::State &bm) {
for (auto _ : bm) {
omp_set_num_threads(2);
#pragma omp parallel for
for (size_t i = 0; i < n; i++) {
a[i] = funcC(a[i]);
}
benchmark::DoNotOptimize(a);
}
}
BENCHMARK(BM_2funcC);
void BM_4funcC(benchmark::State &bm) {
for (auto _ : bm) {
omp_set_num_threads(4);
#pragma omp parallel for
for (size_t i = 0; i < n; i++) {
a[i] = funcC(a[i]);
}
benchmark::DoNotOptimize(a);
}
}
BENCHMARK(BM_4funcC);
void BM_6funcC(benchmark::State &bm) {
for (auto _ : bm) {
omp_set_num_threads(6);
#pragma omp parallel for
for (size_t i = 0; i < n; i++) {
a[i] = funcC(a[i]);
}
benchmark::DoNotOptimize(a);
}
}
BENCHMARK(BM_6funcC);
void BM_8funcC(benchmark::State &bm) {
for (auto _ : bm) {
omp_set_num_threads(8);
#pragma omp parallel for
for (size_t i = 0; i < n; i++) {
a[i] = funcC(a[i]);
}
benchmark::DoNotOptimize(a);
}
}
BENCHMARK(BM_8funcC);
void BM_10funcC(benchmark::State &bm) {
for (auto _ : bm) {
omp_set_num_threads(10);
#pragma omp parallel for
for (size_t i = 0; i < n; i++) {
a[i] = funcC(a[i]);
}
benchmark::DoNotOptimize(a);
}
}
BENCHMARK(BM_10funcC);
BENCHMARK_MAIN();
|
经过测试可以看到:
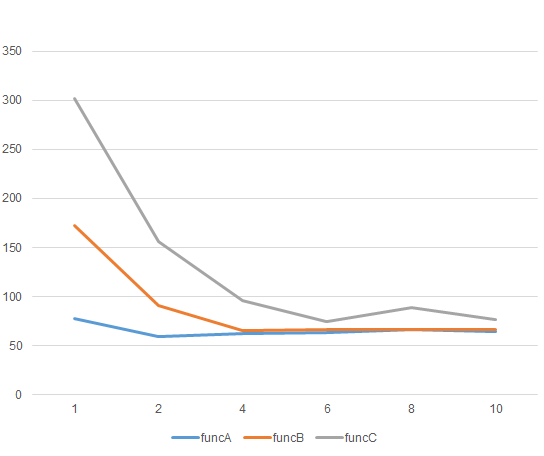
funcA用了2核就饱和。
funcB用了4核才饱和。
funcC用了6核才饱和。
结论:要想利用全部CPU核心,避免mem-bound,需要func里有足够的计算量。
当核心数量越多,CPU计算能力越强,相对之下来不及从内存读写数据,从而越容易mem-bound。
内存信息查看工具:dmidecode
Linux系统查看内存信息:
1
| sudo dmidecode -t memory
|
Windows查看内存信息:
1
| Get-WmiObject Win32_PhysicalMemory
|
- 我此时在WSL2中进行测试,无法使用 dmidecode 因此我只能在Windows中使用Powershell进行测试
- Linux中的输出结果会与下面的不同,请自行测试

可以看到我的电脑上插了两根内存,频率为3200MHz,数据宽度是64位(8字节)
理论极限带宽 = 频率 * 位宽 * 数量(其实是通道数)
1
| 3200 * 8 * 2 = 51200 MB/s = 51.2 GB/s
|
- 频率相同的情况下,可以考虑插两块8GB的内存,比插一块16GB的内存更快
- 系统会自动在两者之间均匀分配内存,保证读写均匀分配到两个内存上,实现内存的并行读写,这和磁盘 RAID 有一定相似之处。
验证 parallel_add 是否充分利用了带宽
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
| #include <benchmark/benchmark.h>
#include <omp.h>
#include <x86intrin.h>
#include <array>
#include <cmath>
#include <cstdlib>
#include <cstring>
#include <iostream>
#include <vector>
constexpr size_t n = 1 << 28;
std::vector<float> a(n);
void BM_parallel_add(benchmark::State &bm) {
for (auto _ : bm) {
#pragma omp parallel for
for (size_t i = 0; i < n; i++) {
a[i] = a[i] + 1;
}
benchmark::DoNotOptimize(a);
}
}
BENCHMARK(BM_parallel_add);
BENCHMARK_MAIN();
|
在这个例子中,我们使用了 1GB 的数据量(即 1024MB)。每次操作不仅需要读取数组 a,还要将计算结果写回,实际上传输了 2GB 的数据(即 2048MB)。
总耗时为 0.142888 秒,因此带宽为:
1
| 带宽 = 2048MB / 0.142888s ≈ 14332 MB/s
|
然而,这个带宽显著低于理论最大带宽,原因可能涉及多种因素。
- 正常也不会出现这么大的差距,我在 WSL 环境下运行,可能会存在性能上的额外开销。
第二章:缓存与局域性
不同数据量对带宽的影响
进一步分析带宽的表现,我们尝试不同大小的数据量来测试带宽变化。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
| #include <benchmark/benchmark.h>
#include <omp.h>
#include <x86intrin.h>
#include <array>
#include <cmath>
#include <cstdlib>
#include <cstring>
#include <iostream>
#include <vector>
constexpr size_t n = 1 << 28;
std::vector<float> a(n);
void BM_fill1GB(benchmark::State &bm) {
for (auto _ : bm) {
for (size_t i = 0; i < (1 << 28); i++) {
a[i] = 1;
}
}
}
BENCHMARK(BM_fill1GB);
void BM_fill128MB(benchmark::State &bm) {
for (auto _ : bm) {
for (size_t i = 0; i < (1 << 25); i++) {
a[i] = 1;
}
}
}
BENCHMARK(BM_fill128MB);
void BM_fill16MB(benchmark::State &bm) {
for (auto _ : bm) {
for (size_t i = 0; i < (1 << 22); i++) {
a[i] = 1;
}
}
}
BENCHMARK(BM_fill16MB);
void BM_fill1MB(benchmark::State &bm) {
for (auto _ : bm) {
for (size_t i = 0; i < (1 << 18); i++) {
a[i] = 1;
}
}
}
BENCHMARK(BM_fill1MB);
void BM_fill128KB(benchmark::State &bm) {
for (auto _ : bm) {
for (size_t i = 0; i < (1 << 15); i++) {
a[i] = 1;
}
}
}
BENCHMARK(BM_fill128KB);
void BM_fill16KB(benchmark::State &bm) {
for (auto _ : bm) {
for (size_t i = 0; i < (1 << 12); i++) {
a[i] = 1;
}
}
}
BENCHMARK(BM_fill16KB);
BENCHMARK_MAIN();
|
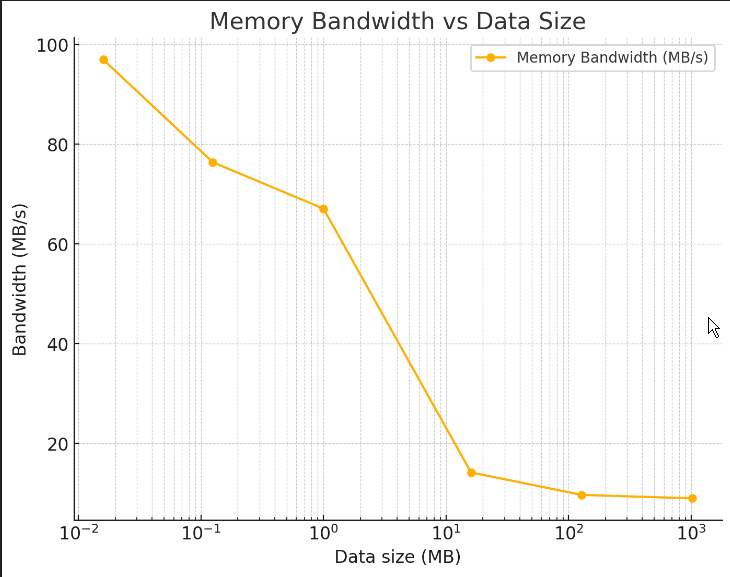
结果分析:
可以看到,当数据量较小时,实际带宽反而超出了理论带宽。这是因为较小的数据集能够完全缓存到 CPU 的高速缓存中,避免了从内存访问的瓶颈。
当数据量增加时,带宽逐渐趋近于理论带宽,特别是数据量大到无法完全装入 L1 和 L2 缓存时,性能受限于内存带宽。
CPU内部的高速缓存
CPU 厂商早已认识到内存延迟较高的问题,因此在 CPU 内部引入了多个级别的缓存,以减少访问内存时的延迟。缓存通常分为三级:
- L1 缓存:速度最快,容量较小,通常为 32KB(每个核心独立)。
- L2 缓存:较 L1 缓存大,约为 512KB(每个核心独立)。
- L3 缓存:最大,通常为 8MB 到 16MB,所有核心共享。
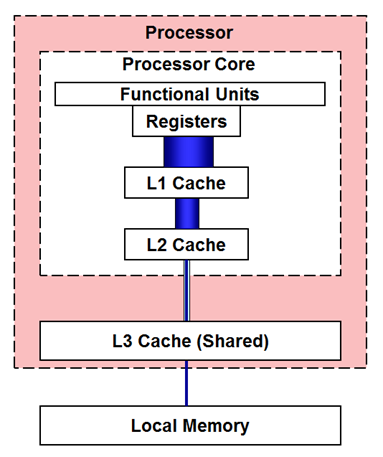
CPU 缓存的工作原理
当 CPU 请求数据时,它首先检查 L1 缓存。如果数据不在 L1 缓存中,它会检查 L2 缓存,然后是 L3 缓存,最后从主内存加载。如果数据已经缓存,则直接从缓存中读取,显著减少访问延迟。
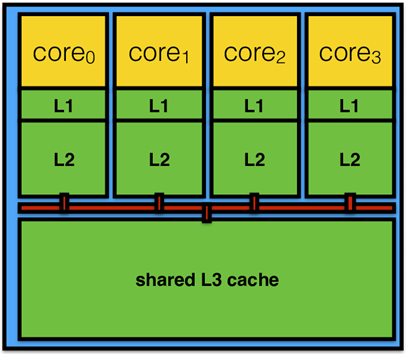
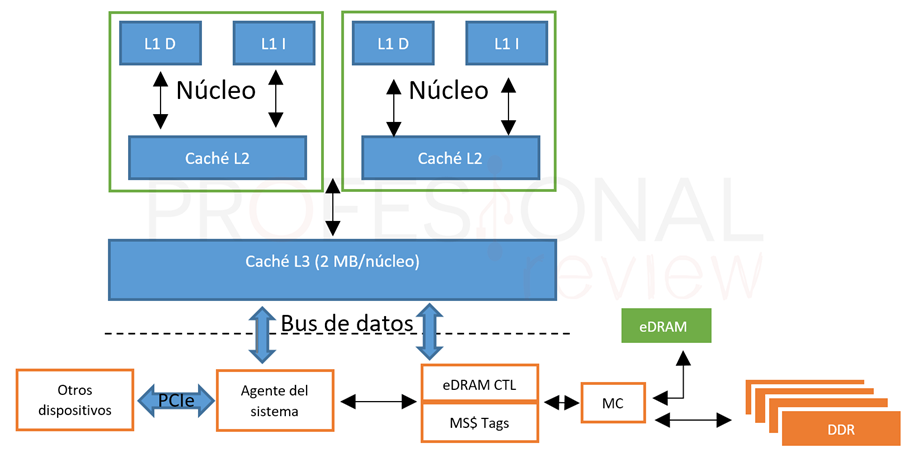
缓存的分级结构
注意,从下图我们可以看到,L1和L2缓存是每个核心都有一个,L3才是多个核心共用。
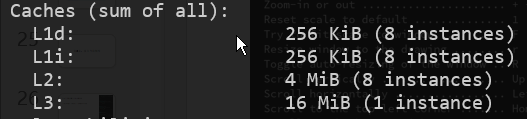
查看高速缓存大小:lscpu
可以看到我们 x86 电脑的缓存结构分为三级:
一级缓存分为数据缓存和指令缓存,其中数据缓存有 32 KB,8 个物理核心每个都有一个,总共 256 KB。而指令缓存的大小刚好和数据缓存一样也是 256 KB。
二级缓存有 512 KB,8 个物理核心每个都有一个,总共 4 MB。
三级缓存由各个物理核心共享,总共 16 MB。
通过图形界面查看拓扑结构:lstopo
如何分析带宽测试结果
可以看到刚刚两个出现转折的点,也是在二级缓存和三级缓存的大小附近。

根据上面的图表,可以观察到在特定数据量下(如 128KB 到 16MB 区间),性能出现了转折点。这正是由于 CPU 缓存大小的影响:
- 当数据小到可以完全装入 L2 缓存 时,带宽接近 L2 缓存的带宽限制。
- 当数据量较大时,无法完全存入缓存,带宽受限于 L3 缓存 或主内存带宽。
结论:要避免mem-bound,数据量尽量足够小,如果能装的进缓存就高效了。
缓存的工作机制:读取操作
缓存中的数据结构如下:
1
2
3
4
5
6
| struct CacheEntry {
bool valid;
uint64_t address;
char data[64];
};
CacheEntry cache[512];
|
当 CPU 请求读取一个地址时,缓存会检查是否存在与该地址匹配的条目。如果找到匹配项,则直接从缓存返回数据;如果没有找到,则向主内存发起读取请求,获取该地址的数据并创建一个新的缓存条目。
在 x86 架构中,每个缓存条目存储 64 字节数据,这也称为一个 缓存行(cacheline)。
例如,当 CPU 访问地址 0x0048~0x0050(即 4 字节)时,实际上会将从地址 0x0040 到 0x0080 范围内的 64 字节数据读取到缓存中。
这就是为什么我们喜欢把数据结构的起始地址和大小对齐到 64 字节,这样可以避免浪费缓存行的存储空间。
缓存的工作机制:写操作
当 CPU 向某个地址写入数据时,缓存会查找是否已有匹配的条目。如果找到,则直接修改缓存中的数据;如果没有找到,则会创建一个新的缓存条目来存储写入的数据,并将其标记为“脏”数据(dirty)。这意味着数据已经修改,但尚未写回主内存。
当读和写创建的新条目过多,缓存快要塞不下时,他会把最不常用的那个条目移除,这个现象称为失效(invalid)。如果那个条目是被标记为脏的,则说明是当时打算写入的数据,那就需要向主内存发送写入请求,等他写入成功,才能安全移除这个条目。
在多级缓存的情况下,如果一级缓存的条目被失效,它可能会被推送到二级缓存中。
连续访问与跨步访问
如果访问数组时,按一定的间距跨步访问,则效率如何?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
| #include <benchmark/benchmark.h>
#include <iostream>
#include <vector>
constexpr size_t n = 1 << 28;
std::vector<float> a(n);
void BM_skip1(benchmark::State &bm) {
for (auto _ : bm) {
#pragma omp parallel for
for (size_t i = 0; i < n; i += 1) {
a[i] = 1;
}
benchmark::DoNotOptimize(a);
}
}
BENCHMARK(BM_skip1);
void BM_skip2(benchmark::State &bm) {
for (auto _ : bm) {
#pragma omp parallel for
for (size_t i = 0; i < n; i += 2) {
a[i] = 1;
}
benchmark::DoNotOptimize(a);
}
}
BENCHMARK(BM_skip2);
void BM_skip4(benchmark::State &bm) {
for (auto _ : bm) {
#pragma omp parallel for
for (size_t i = 0; i < n; i += 4) {
a[i] = 1;
}
benchmark::DoNotOptimize(a);
}
}
BENCHMARK(BM_skip4);
void BM_skip8(benchmark::State &bm) {
for (auto _ : bm) {
#pragma omp parallel for
for (size_t i = 0; i < n; i += 8) {
a[i] = 1;
}
benchmark::DoNotOptimize(a);
}
}
BENCHMARK(BM_skip8);
void BM_skip16(benchmark::State &bm) {
for (auto _ : bm) {
#pragma omp parallel for
for (size_t i = 0; i < n; i += 16) {
a[i] = 1;
}
benchmark::DoNotOptimize(a);
}
}
BENCHMARK(BM_skip16);
void BM_skip32(benchmark::State &bm) {
for (auto _ : bm) {
#pragma omp parallel for
for (size_t i = 0; i < n; i += 32) {
a[i] = 1;
}
benchmark::DoNotOptimize(a);
}
}
BENCHMARK(BM_skip32);
void BM_skip64(benchmark::State &bm) {
for (auto _ : bm) {
#pragma omp parallel for
for (size_t i = 0; i < n; i += 64) {
a[i] = 1;
}
benchmark::DoNotOptimize(a);
}
}
BENCHMARK(BM_skip64);
void BM_skip128(benchmark::State &bm) {
for (auto _ : bm) {
#pragma omp parallel for
for (size_t i = 0; i < n; i += 128) {
a[i] = 1;
}
benchmark::DoNotOptimize(a);
}
}
BENCHMARK(BM_skip128);
BENCHMARK_MAIN();
|
在跨步从 1 到 16 时,访问效率差别不大,但从 32 开始,跨步增大才可以效率变快,而且变化呈现出以 2 的倍数递增的趋势。为什么会出现这种情况?
在跨步从 1 到 16 时,性能差异较小,这是因为访问的跨度都小于 64 字节(即一个缓存行的大小)。每次访问会加载整个缓存行,因此即使跨步增大,仍然需要读取相同的数据区域。
因为CPU和内存之间隔着缓存,而缓存和内存之间传输数据的最小单位是缓存行(64字节)。16 个 float 类型数据正好等于 64 字节,所以小于64字节的跨步访问,实际上这个数组的所有区域都被加载了一遍,因此并没有起到减少内存访问次数的效果。
只有超过64字节的跨步,中间的那个缓存行才不会被读取,实际上才减少了内存访问次数,因此变快了。
- 至于从128步幅(512字节)之后的效果,就需要考虑多级缓存的原因
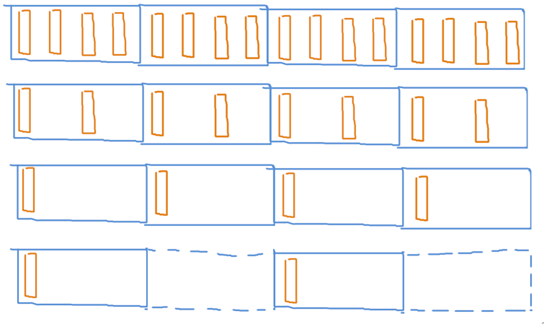
缓存行决定数据的粒度
结论:访问内存的用时,和访问的字节数量无关,和访问的每个字节所在的缓存行数量有关。
可见,能否很好的利用缓存,和程序访问内存的空间局域性有关。
所以我们设计数据结构时,应该把数据存储的尽可能紧凑,不要松散排列。最好每个缓存行里要么有数据,要么没数据,避免读取缓存行时浪费一部分空间。
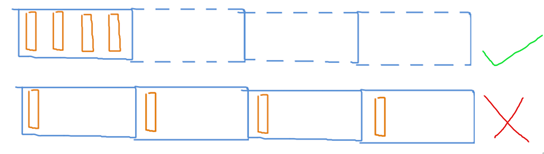
结构体布局分析
- 结构体的基础布局
定义一个结构体 MyClass:
1
2
3
4
5
6
7
| struct MyClass{
float x;
float y;
float z;
};
MyClass mc;
|
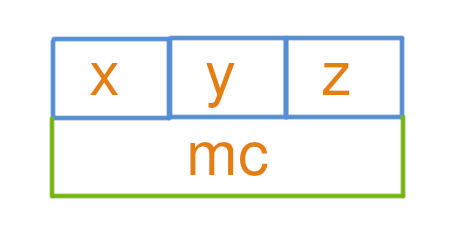
- AOS(Array of Struct)模式
在 AOS 模式下,每个对象的属性存储在一起:
1
2
3
4
5
6
7
| struct MyClass{
float x;
float y;
float z;
};
MyClass mc[4];
|
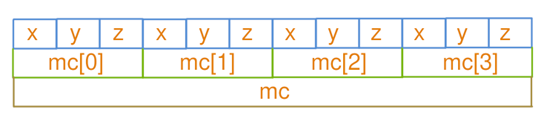
或者使用vector:
1
2
3
4
5
6
7
| struct MyClass{
float x;
float y;
float z;
};
std::vector<MyClass> mc(4);
|
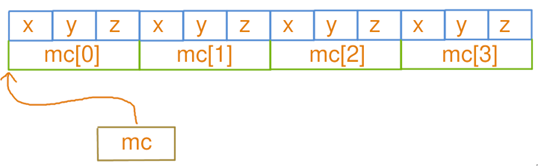
- SOA(Struct of Array)模式
在 SOA 模式下,各属性分开存储在独立的数组中:
1
2
3
4
5
6
7
| struct MyClass{
float x[4];
float y[4];
float z[4];
};
MyClass mc;
|

AOS 与 SOA 的内存布局差异
- AOS(Array of Struct)单个对象的属性紧挨着存:

- SOA(Struct of Array)属性分离存储在多个数组:

AOS 必须对齐到 2 的幂才高效,SOA 就不需要。
AOS 符合直觉,不一定要存储在数组这种线性结构,而 SOA 可能无法保证多个数组大小一致。
SOA 不符合直觉,但通常是更高效的!

AOS 和 SOA 的性能对比
在以下代码中进行 AOS 与 SOA 访问的性能基准测试:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
| constexpr size_t n = 1 << 26;
void BM_aos(benchmark::State &bm) {
struct MyClass {
float x;
float y;
float z;
};
std::vector<MyClass> mc(n);
for (auto _ : bm) {
#pragma omp parallel for
for (size_t i = 0; i < n; i++) {
mc[i].x = mc[i].x + mc[i].y;
}
benchmark::DoNotOptimize(mc);
}
}
BENCHMARK(BM_aos);
void BM_soa(benchmark::State &bm) {
std::vector<float> mc_x(n);
std::vector<float> mc_y(n);
std::vector<float> mc_z(n);
for (auto _ : bm) {
#pragma omp parallel for
for (size_t i = 0; i < n; i++) {
mc_x[i] = mc_x[i] + mc_y[i];
}
benchmark::DoNotOptimize(mc_x);
benchmark::DoNotOptimize(mc_y);
benchmark::DoNotOptimize(mc_z);
}
}
BENCHMARK(BM_soa);
|
因为缓存行大小是64字节,它是从内存读写的最小单位。
而这里的AOS,它的MyClass有三个float,大小仅为12字节。
所以当修改MyClass的x属性时,必须读取整个MyClass,仅仅修改其中的x属性,然后写回。这就浪费了:y的写、z的写、z的读。实际用上的只有:x的读,y的读,x的写。浪费了50%带宽。
而SOA把三个属性分开存,每个属性作为独立的数组,稠密存储。这样当用不到z的时候,z数组就完全不会被读取,不会占用内存带宽,从而带宽利用率是100%,因此比AOS快了3倍。
AOSOA:结合 AOS 与 SOA 优势

可以采用 AOS 外层结构,内部 SOA 的方式组织数据,即 AOSOA。这种布局在高层次上是 AOS,但每个元素内部分为 SOA。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
| void BM_aosoa(benchmark::State &bm) {
struct MyClass {
float x[1024];
float y[1024];
float z[1024];
};
std::vector<MyClass> mc(n / 1024);
for (auto _ : bm) {
#pragma omp parallel for
for (size_t i = 0; i < n / 1024; i++) {
#pragma omp simd
for (size_t j = 0; j < 1024; j++) {
mc[i].x[j] = mc[i].x[j] + mc[i].y[j];
}
}
benchmark::DoNotOptimize(mc);
}
}
BENCHMARK(BM_aosoa);
|
缺点是必须保证数量是 1024 的整数倍,而且因为要两次指标索引,随机访问复杂度较高。
这里的 1024 并非随意选取,而是要让每个属性 SOA 数组的大小为一个页(4KB)才能最高效,原因稍后会说明。
注意,内部SOA的尺寸不宜太小
如果内部SOA太小,内部循环只有16次连续的读取,16次结束后就会跳跃一段,然后继续连续的读取。这会导致CPU预取机制失效,无法预测下一次要读哪里,等发现跳跃时已经来不及了,从而计算的延迟无法隐藏。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
| void BM_aosoa_16(benchmark::State &bm) {
struct MyClass {
float x[16];
float y[16];
float z[16];
};
std::vector<MyClass> mc(n / 16);
for (auto _ : bm) {
#pragma omp parallel for
for (size_t i = 0; i < n / 16; i++) {
#pragma omp simd
for (size_t j = 0; j < 16; j++) {
mc[i].x[j] = mc[i].x[j] + mc[i].y[j];
}
}
benchmark::DoNotOptimize(mc);
}
}
BENCHMARK(BM_aosoa_16);
|
如果每个属性都要访问到,那还是AOS比较好(AOSOA也不赖)
这是因为使用SOA会让CPU不得不同时维护很多条预取赛道(mc_x, mc_y, mc_z),当赛道多了以后每一条赛道的长度就变短了,从而能够周转的余地时间比较少,不利于延迟隐藏。
而如果把这三条赛道合并成一条(mc),这样同样的经费(缓存容量)能铺出的赛道(预取)就更长,从而CPU有更长的周转时间来隐藏他内部计算的延迟。所以本案例中AOS比SOA好。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
| #include <benchmark/benchmark.h>
#include <omp.h>
#include <x86intrin.h>
#include <array>
#include <cmath>
#include <cstdlib>
#include <cstring>
#include <iostream>
#include <vector>
constexpr size_t n = 1 << 26;
void BM_aos(benchmark::State &bm) {
struct MyClass {
float x;
float y;
float z;
};
std::vector<MyClass> mc(n);
for (auto _ : bm) {
#pragma omp parallel for
for (size_t i = 0; i < n; i++) {
mc[i].x += 1;
mc[i].y += 1;
mc[i].z += 1;
}
benchmark::DoNotOptimize(mc);
}
}
BENCHMARK(BM_aos);
void BM_soa(benchmark::State &bm) {
std::vector<float> mc_x(n);
std::vector<float> mc_y(n);
std::vector<float> mc_z(n);
for (auto _ : bm) {
#pragma omp parallel for
for (size_t i = 0; i < n; i++) {
mc_x[i] += 1;
mc_y[i] += 1;
mc_z[i] += 1;
}
benchmark::DoNotOptimize(mc_x);
benchmark::DoNotOptimize(mc_y);
benchmark::DoNotOptimize(mc_z);
}
}
BENCHMARK(BM_soa);
void BM_aosoa(benchmark::State &bm) {
struct MyClass {
float x[1024];
float y[1024];
float z[1024];
};
std::vector<MyClass> mc(n / 1024);
for (auto _ : bm) {
#pragma omp parallel for
for (size_t i = 0; i < n / 1024; i++) {
#pragma omp simd
for (size_t j = 0; j < 1024; j++) {
mc[i].x[j] += 1;
mc[i].y[j] += 1;
mc[i].z[j] += 1;
}
}
benchmark::DoNotOptimize(mc);
}
}
BENCHMARK(BM_aosoa);
BENCHMARK_MAIN();
|
结论:AOS、SOA、AOSOA 哪家强
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
|
struct ParticleList {
std::vector<float> pos_x;
std::vector<float> pos_y;
std::vector<float> pos_z;
std::vector<float> vel_x;
std::vector<float> vel_y;
std::vector<float> vel_z;
};
struct ParticleList {
std::vector<glm::vec3> pos;
std::vector<glm::vec3> vel;
};
struct ParticleBlock {
float pos_x[1024];
float pos_y[1024];
float pos_z[1024];
float vel_x[1024];
float vel_y[1024];
float vel_z[1024];
};
using ParticleList = std::vector<ParticleBlock>;
struct Particle {
glm::vec3 pos;
glm::vec3 vel;
};
using ParticleList = std::vector<Particle>;
|
若多个属性(如 pos.x, pos.y, pos.z)总是一起使用,可能都是同时读取同时修改的,AOS 可以减少预取压力。
当属性中有些并不总是一起访问或写入时,例如 pos 和 vel,通常 pos+=vel 的操作中 pos 是读写,而 vel 仅为只读,此时 SOA 更适合,因为能减少内存带宽的占用。
将 pos 的 x、y、z 分量使用 AOS 存储这个结论是单从内存访问效率来看的,但需要SIMD矢量化(例如 hw04 的情况),SOA或AOSOA可能更合适。
不过,对于非连续存储结构,如带有索引开销的稀疏哈希网格,SOA 可能并不适用。
AOSOA :在高层保留 AOS 的统一索引,同时在底层享受 SOA 带来的矢量化和缓存行预取优势,只是随机访问的复杂度更高。。。
第三章:预取与直写
顺序访问与随机访问
随机访问的效率比顺序访问低的多。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
| #include <benchmark/benchmark.h>
#include <omp.h>
#include <x86intrin.h>
#include <array>
#include <cmath>
#include <cstdlib>
#include <cstring>
#include <iostream>
#include <vector>
constexpr size_t n = 1 << 27;
std::vector<float> a(n);
void BM_ordered(benchmark::State &bm) {
for (auto _ : bm) {
#pragma omp parallel for
for (size_t i = 0; i < n; i++) {
benchmark::DoNotOptimize(a[i]);
}
benchmark::DoNotOptimize(a);
}
}
BENCHMARK(BM_ordered);
static uint32_t randomize(uint32_t i) {
i = (i ^ 61) ^ (i >> 16);
i *= 9;
i ^= i << 4;
i *= 0x27d4eb2d;
i ^= i >> 15;
return i;
}
void BM_random(benchmark::State &bm) {
for (auto _ : bm) {
#pragma omp parallel for
for (size_t i = 0; i < n; i++) {
size_t r = randomize(i) % n;
benchmark::DoNotOptimize(a[r]);
}
benchmark::DoNotOptimize(a);
}
}
BENCHMARK(BM_random);
BENCHMARK_MAIN();
|
其中一个原因当然是:随机访问只会访问到其中一个float,而这导致他附近的64字节都被读取到缓存了,但实际只用到了其中4字节,之后又没用到剩下的60字节,导致浪费了94%的带宽。
虽说连续、顺序访问是最理想的,然而在使用哈希表等数据结构中,不可避免的会通过哈希函数得到随机的地址来访问,且Value类型可能小于64字节,浪费部分带宽。怎么办?
解决:按64字节分块地随机访问
解决方法就是,把数据按64字节大小分块。随机访问时,只随机块的位置,而块的内部仍然按顺序访问。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
| #include <benchmark/benchmark.h>
#include <omp.h>
#include <x86intrin.h>
#include <array>
#include <cmath>
#include <cstdlib>
#include <cstring>
#include <iostream>
#include <vector>
constexpr size_t n = 1 << 27;
std::vector<float> a(n);
static uint32_t randomize(uint32_t i) {
i = (i ^ 61) ^ (i >> 16);
i *= 9;
i ^= i << 4;
i *= 0x27d4eb2d;
i ^= i >> 15;
return i;
}
void BM_ordered(benchmark::State &bm) {
for (auto _ : bm) {
#pragma omp parallel for
for (size_t i = 0; i < n; i++) {
benchmark::DoNotOptimize(a[i]);
}
benchmark::DoNotOptimize(a);
}
}
BENCHMARK(BM_ordered);
void BM_random_4B(benchmark::State &bm) {
for (auto _ : bm) {
#pragma omp parallel for
for (size_t i = 0; i < n; i++) {
size_t r = randomize(i) % n;
benchmark::DoNotOptimize(a[r]);
}
benchmark::DoNotOptimize(a);
}
}
BENCHMARK(BM_random_4B);
void BM_random_64B(benchmark::State &bm) {
for (auto _ : bm) {
#pragma omp parallel for
for (size_t i = 0; i < n / 16; i++) {
size_t r = randomize(i) % (n / 16);
for (size_t j = 0; j < 16; j++) {
benchmark::DoNotOptimize(a[r * 16 + j]);
}
}
benchmark::DoNotOptimize(a);
}
}
BENCHMARK(BM_random_64B);
BENCHMARK_MAIN();
|
可以看到64字节分块的效果拔群,但还是比顺序访问慢一些,为什么?明明没有浪费带宽了?
缓存行预取技术:吃着一碗饭的同时,先喊妈妈烧下一碗饭
其实,当程序顺序访问 a[0], a[1] 时,CPU会智能地预测到你接下来可能会读取 a[2],于是会提前给缓存发送一个读取指令,让他读取 a[2]、a[3]。缓存在后台默默读取数据的同时,CPU自己在继续处理 a[0] 的数据。这样等 a[0], a[1] 处理完以后,缓存也刚好读取完 a[2] 了,从而CPU不用等待,就可以直接开始处理 a[2],避免等待数据的时候CPU空转浪费时间。
这种策略称之为预取(prefetch),由硬件自动识别你程序的访存规律,决定要预取的地址。一般来说只有线性的地址访问规律(包括顺序、逆序;连续、跨步)能被识别出来,而如果你的访存是随机的,那就没办法预测。遇到这种突如其来的访存时,CPU不得不空转等待数据的抵达才能继续工作,浪费了时间。
解决:按更大的分块(4096字节)随机访问
还可以把分块的大小调的更大一些,比如 4KB 那么大,即64个缓存行,而不是一个。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
|
void BM_random_4KB(benchmark::State &bm) {
for (auto _ : bm) {
#pragma omp parallel for
for (size_t i = 0; i < n / 1024; i++) {
size_t r = randomize(i) % (n / 1024);
for (size_t j = 0; j < 1024; j++) {
benchmark::DoNotOptimize(a[r * 1024 + j]);
}
}
benchmark::DoNotOptimize(a);
}
}
BENCHMARK(BM_random_4KB);
|
这样一次随机访问之后会伴随着64次顺序访问,能被CPU检测到,从而启动缓存行预取,避免了等待数据抵达前空转浪费时间。
页对齐的重要性
为什么要 4KB,能不能更大一些?
来现在操作系统管理内存是用分页(page),程序的内存是一页一页贴在地址空间中的,有些地方可能不可访问,或者还没有分配,则把这个页设为不可用状态,访问他就会出错,进入内核模式。
因此硬件出于安全,预取不能跨越页边界,否则可能会触发不必要的 page fault。所以我们选用页的大小,因为本来就不能跨页顺序预取,所以被我们切断掉也无所谓。
另外,我们可以用 _mm_alloc 申请起始地址对齐到页边界的一段内存,真正做到每个块内部不出现跨页现象。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
|
void BM_random_4KB_aligned(benchmark::State &bm) {
float *a = (float *)_mm_malloc(n * sizeof(float), 4096);
memset(a, 0, n * sizeof(float));
for (auto _ : bm) {
#pragma omp parallel for
for (size_t i = 0; i < n / 1024; i++) {
size_t r = randomize(i) % (n / 1024);
for (size_t j = 0; j < 1024; j++) {
benchmark::DoNotOptimize(a[r * 1024 + j]);
}
}
benchmark::DoNotOptimize(a);
}
_mm_free(a);
}
BENCHMARK(BM_random_4KB_aligned);
|
手动预取:_mm_prefetch
对于不得不随机访问很小一块的情况,还可以通过 _mm_prefetch 指令手动预取一个缓存行。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
|
void BM_random_64B(benchmark::State &bm) {
for (auto _ : bm) {
#pragma omp parallel for
for (size_t i = 0; i < n / 16; i++) {
size_t r = randomize(i) % (n / 16);
for (size_t j = 0; j < 16; j++) {
benchmark::DoNotOptimize(a[r * 16 + j]);
}
}
benchmark::DoNotOptimize(a);
}
}
BENCHMARK(BM_random_64B);
void BM_random_64B_prefetch(benchmark::State &bm) {
for (auto _ : bm) {
#pragma omp parallel for
for (size_t i = 0; i < n / 16; i++) {
size_t next_r = randomize(i + 64) % (n / 16);
_mm_prefetch(&a[next_r * 16], _MM_HINT_T0);
size_t r = randomize(i) % (n / 16);
for (size_t j = 0; j < 16; j++) {
benchmark::DoNotOptimize(a[r * 16 + j]);
}
}
benchmark::DoNotOptimize(a);
}
}
BENCHMARK(BM_random_64B_prefetch);
BENCHMARK_MAIN();
|
这里第一个参数是要预取的地址(最好对齐到缓存行),第二个参数 _MM_HINT_T0 代表预取数据到一级缓存,_MM_HINT_T1 代表只取到二级缓存,_MM_HINT_T2 代表三级缓存;_MM_HINT_NTA 则是预取到非临时缓冲结构中,可以最小化对缓存的污染,但是必须很快被用上。
重新理解 mem-bound:延迟隐藏
之前提到,1次浮点读写必须伴随着32次浮点加法的运算量,否则和只有0次加法的耗时没有任何区别,即内存带宽成唯一瓶颈的mem-bound。可是按我们理解,“1次读写+0次加法”应该会比“1次读写+8次加法”快一点点吧,因为8次加法尽管比1次读写快很多,但是毕竟还是有时间的啊,为什么会几乎没有任何区别?
这都是得益于CPU的预取机制,他能够在等待a[i+1]的内存数据抵达时,默默地做着a[i]的计算,从而只要计算的延迟小于内存的延迟,延迟就被隐藏起来了,而不必等内存抵达了再算。这就是为什么有些运算量不足32次的程序还是会无法达到mem-bound,手动预取以后才能达到,就是因为硬件预取预测失败,导致不得不等内存抵达了才能算,导致延迟隐藏失败。隐藏成功:
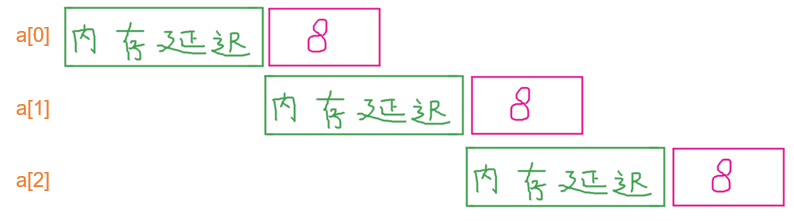
为什么写入比读取慢?